Imaging Black Holes

During the summer of 2020, I participated in the REU program at the University of California, Davis. I worked on a project imaging black holes in four and five dimensions. There are two questions that come up when I tell people about the project. One, why? And two, what do you mean five dimensions? The goal of this post is to try to explain my work to a the average person who is willing to spend the time to learn about some high level physics. To answer the first question we must first discuss the AdS/CFT correspondence.

Background

The AdS/CFT correspondence stands for the Anti-de Sitter Conformal Field theory correspondence. The correspondence relates an Anti-de Sitter spacetime to a conformal field theory defined on its boundary. What exactly does that mean?

Let’s start with Anti-de Sitter space. We can think of our world as existing within a four dimensional spacetime with three spatial directions and one time direction. The room you are in would be consider a flat spacetime. The fastest way for you to move across the room would be to walk in a straight line. The fastest way for you to move through time relative to the room is to sit still. If you have ever seen maps of flights that travel long distances over the earth you may have noticed that lines are not straight. Unlike the room you are in, the earth is not flat. Therefore, for a plane to use the minimum amount of fuel per flight it must travel the shortest distance for itself. On a map of the earth that is projected to be flat, the shortest distance may look like a straight line. But for a plane, the shortest distance for it to travel between two points on earth is to follow the path of a great circle or more generally know as a geodesic. The spacetime I am working in, Anti-de Sitter spacetime, has the exact opposite properties of a spacetime defined on a sphere, i.e. the opposite of walking around on earth. This is a weird concept to comprehend and it is not necessary to understand my work. However, if you are interested I’ll link to a great video explaining what the world might look like in hyperbolic geometry. But the curvature of the spacetime does explain the difference in the shape of black holes I imaged. These spacetime are physically outside the realm of human experience. You may ask, “Why then study them?” And the answer is simple: because math.

The AdS/ CFT correspondence is fundamentally a mathematical relation. Without getting into too many details, Field Theories are convenient ways of representing particles and their interactions. The Standard Model of Particle Physics is such a field theory. Conformal Field Theories (CFT) are a subset of Field Theories that have special mathematical properties. Without getting into these properties, the AdS/ CFT correspondence relates how particles would interact in AdS space with how they would interact in a CFT. The caveat is the CFT is only located on the boundary of the AdS space. Let’s simplify. Imagine three men are chained to the floor facing the back of a cave. For their entire lives, they view the world as shadows on the wall of their cave. One day, one man breaks free and leaves the cave. The man is shocked at the sight of the 3-dimensional world. He is now able to experiment in this new landscape and understand how the shadows are made. For example, the man had always watched the shadow of birds defy gravity. Now he can see how the birds are able to extend their wings and glide off the air. By increasing the dimensions of his reality, the man gains a deeper understanding of the physics behind his world. Plato’s Allegory of the Cave illustrates the explanatory power of viewing the world in higher dimensions. This is in essence the AdS/CFT correspondence.

Now onto Black Holes. Einstein’s theory of General Relativity shows that warps space leads to gravitation interaction. When the warping of spacetime become so extreme the forces that are generated become so great that light, the lightest fastest particle in the universe, cannot even escape the gravitational trap. Often time when depicting spacetime around a black hole, illustrations will show only the warping of spacetime in the spatial directions. But, time itself also becomes warped. Illustrated below is the spacetime of a three dimensional black hole, two dimension of space and one dimension of time. The time dimension is shown as the vertical axis where time moves downward. The red cylinder in the middle represents the event horizon of this Black Hole, the place where no light can escape from. The gray cylinder on the outside is the literal edge of the universe. The way this is shown is through a process called compactification. We take the radial coordinate r and run it through a function whose output is between 0 and 1. Explicitly we run the radial coordinate through the hyperbolic tangent, . So when we look at the diagram below we are looking at the universe from its center to infinity. Lastly, the blue surface shows all possible paths that a light particle can travel within this universe.

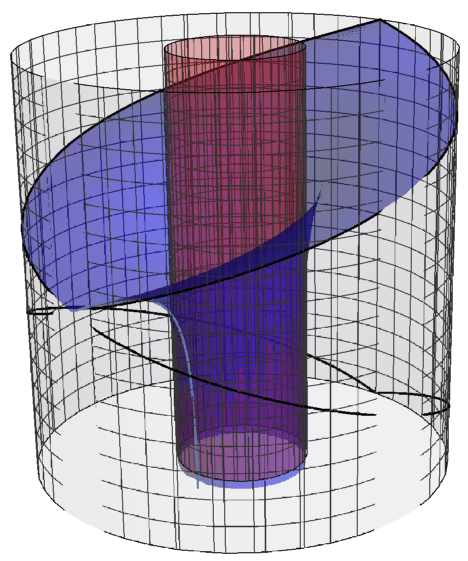
As particles move around in spacetime they follow the shortest path through spacetime, a geodesic. This only applies for particles that are moving through and inertial frame, i.e. they are not accelerating under their own or external power. For example, sitting in the room you are currently sitting you are moving in a straight line through time. A ball falling off a cliff would appear to move along a straight line on a plot of it’s height versus time. Gravity as a force is particles following geodesics through spacetime. It is only the earth’s surface which is preventing us from falling through to earth’s core that pushes back on us and we are able to feel as gravity.

Imaging

For most of the math and methods in this next section I followed the methodology from this paper. At the bottom of this post I’ll link to my REU final report for those who want to know more.

In order to begin imaging a Black Hole we first need to understand how to image space when there isn’t a black hole there, i.e empty space. While looking straight forward, split your view into four equal quadrants. Imagine coloring each quadrant a different color. Each color will represent the quadrant of space behind the black hole where the light hitting your eyes is coming from. The reason we need to partition space in this way is because the path that light travels is affected by the gravity of a black hole. Below is the color scheme I chose to color empty space.

The next step in imaging a black hole is to determine how light would move around it since black holes emit no light from their surface. We then need to create a camera senor in our simulation. The camera sensor would essentially map every point in our colored space back to a 2D image. A normal camera would need to take into account for every ray of light that would hit it’s sensor. If we assume that like is coming from all direction we would therefore need to simulated an infinite amount of light rays in our simulation. Instead, I used the fact that light traveling through space would follow the same path forward as it would backwards. So, if we reverse time and send rays of light out of the camera sensor we could follow their paths to where they continue to off to infinity. We then reverse the process and our image would be where the light rays ended. The inspiration for this method originally came from a New York time article describing the recent images of a Black Hole by the Event Horizon Telescope.

I’ll save the more detailed mathematics for the report on the bottom. Now let’s visualize some black holes.

4D Black Holes

We’ll start off with a classic Schwarzschild black hole. Black holes are the simplest objects in the universe. There are only three numbers that can describe a black hole: it’s angular momentum, it’s electric charge, and it’s mass. Unlike other forms of matter where to fully describe an object you need to know the exact position and momentum of every particle within the object, two black holes with these same three parameters cannot be distinguished from one another. In order to have a black hole it must have mass. A Schwarzschild black hole has no angular momentum or electric charge. Below is the image of a Schwarzschild black hole. Here the affect black holes have on the motion of light can be seen. Further away from the black hole light travels along uninterrupted. As the light rays approach closer to the event horizon they are flung off course. The white ring in the image actually represents light that was coming from behind the camera. In order words the light warped fully around the black hole and back towards the camera sensor. In other words, the camera can see itself in the white ring. The black area represents all the light that was unable to reach the camera sensor because the light rays fell behind the event horizon of the black hole.

Next, let’s look at a spinning black hole. Not only does the mass of black holes affect the trajectory of light, so does their spin. As described above, black holes warp spacetime. Not only do black holes’ mass cause spacetime to buckle, but their spin drags spacetime along with them. Depicted below is a Kerr black hole.

The black hole is spinning with its right side moving out of the screen while the left side moves away. As can be seen, the spin of the black hole drags light in it’s direction of spin. What I find most interesting about this image is the chaotic nature of light near the event horizon. There, light from the entire universe is orbiting the black hole.

The next set of images are going to be in lower resolution. This is because as the geometry of the spacetime becomes more complicated it take more computing power to calculate the trajectory of each individual light particle. Therefore, the resolution of these images will drop to 100×100 pixels instead of the 512×512 pixels above.

As mentioned above, the geometry of spacetime greatly affects the motion of light. Next, we will look at black holes in AdS space. A non-rotating black hole appears to be the same as a black hole in flat spacetime. However, when comparing the two, black holes in AdS space appear bigger. This is because the geometry of the space itself is causing a lensing affect on the light particles. Just like how light is focused after passing through a magnifying glass, AdS space causes light to focus to a point. Below is a cross section of our AdS space. The blue dots are pixels on out camera sensor. If we were to focus closely into the blue dots we would see that the blue lines pass perpendicularly through the camera sensor. On this global scale the camera sensor looks curved. This is the complexity of working with hyperbolic geometry. All the blue lines passing though the senor represent light. As can be seen below, even though we are trying to image empty space all rays of light are focused onto one point.

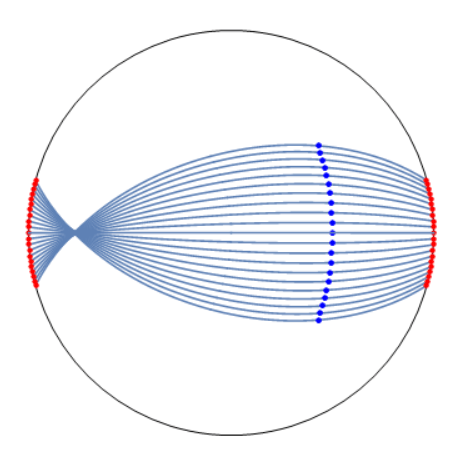
Therefore, the images of black holes will look different from their flat space counterparts. A Schwarzschild black hole simply appears bigger in AdS space so I will omit its image. Kerr black holes however, look drastically different. Below are the images of rotating black holes in AdS space. On the right is a near maximally spinning black hole and on the left is a black hole spinning at half the maximum. Just as there is a maximum speed objects can travel in the universe there is also a maximum rotational speed that objects can spin. As can be seen, as the spin increases the black hole is able to more effectively cut off the left half of the universe from out view.

5D Black Holes

Before we look at five dimensional black holes we must first discuss how we would visualize empty five dimensional space. Remember, one of our spacetime directions is time so the images we are making are static in time. I.e they are images of objects of four spatial directions. But, we unfortunately live in a world with only three spatial directions. So how do we image a four spatial dimensional object.

To start, think back to our image of the Schwarzschild black hole. The black hole was an object of three dimensions yet we were able to visualize it on a 2 dimensional screen. Our minds are used to seeing 3D objects project on a 2D plane. After all, the camera sensors that are our eyes only have a 2D plane of rods and cones to intake all that we see. In order to take a picture of our four dimensional object, we would need a three dimensional camera sensor. Instead of attempting to render a three dimensional object on our screen, I will take the images we generate and slice them along one axis. Just like slicing through a cake, we will be able to see the internal structure our black holes in detail.

Below is an image of empty 4D space. On the left and right are two slices of our 3D image of this space. In the center is a representative black hole. We can image that these 8 octants surround the back of our black hole. Just like in our images above, we had four colors that represented light coming from behind the black hole. With the added dimension, we need to account for this increase in space and need an additional four colors to represent the additional directions light can travel from.

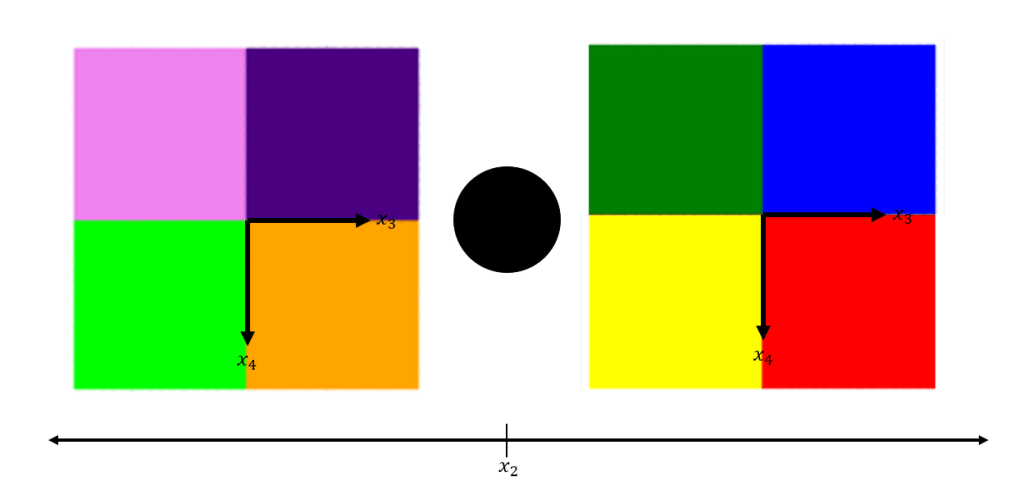
If we were to 3D print this image we would expect the black hole to be in the center of a cube with each octant of the cube colored as represented above.

I’ll end with one last set of images showing what a spinning black hole would look like in five dimensions.

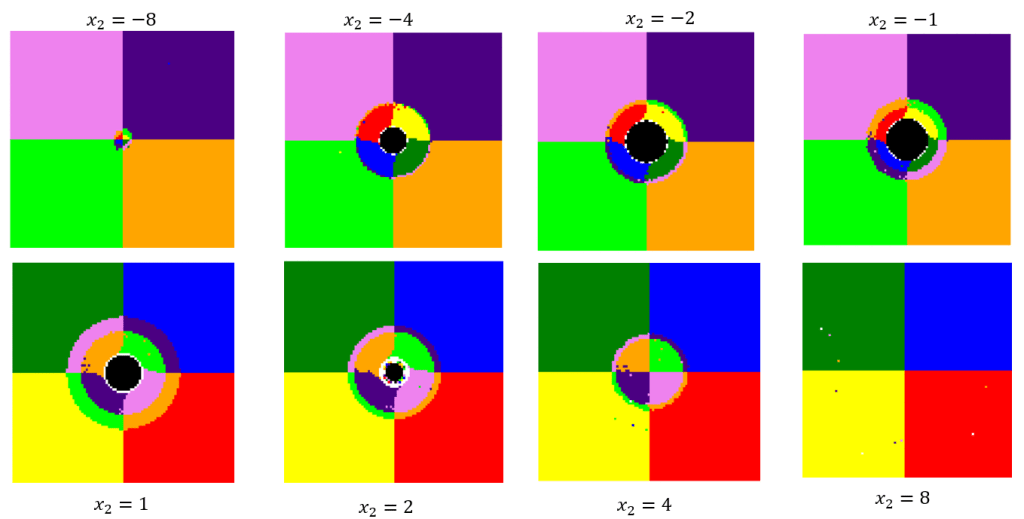
Each plot is a slice of the three dimensional image of the black hole. The labels of these images represent the coordinate that each slice was made from. Viewing these images from left to right, we can see that the black hole would begin to form as we move towards the center of the space. However, we notice that the event horizon is biased towards the left most images. This bias is due to the fact that the black hole is spinning and brings along light from one direction and pushes it away in the other. We also notice the clear warping of light as the we near the event horizon. The warping is in a similar pattern to the four dimensional Kerr black hole shown above.

Thanks for reading!